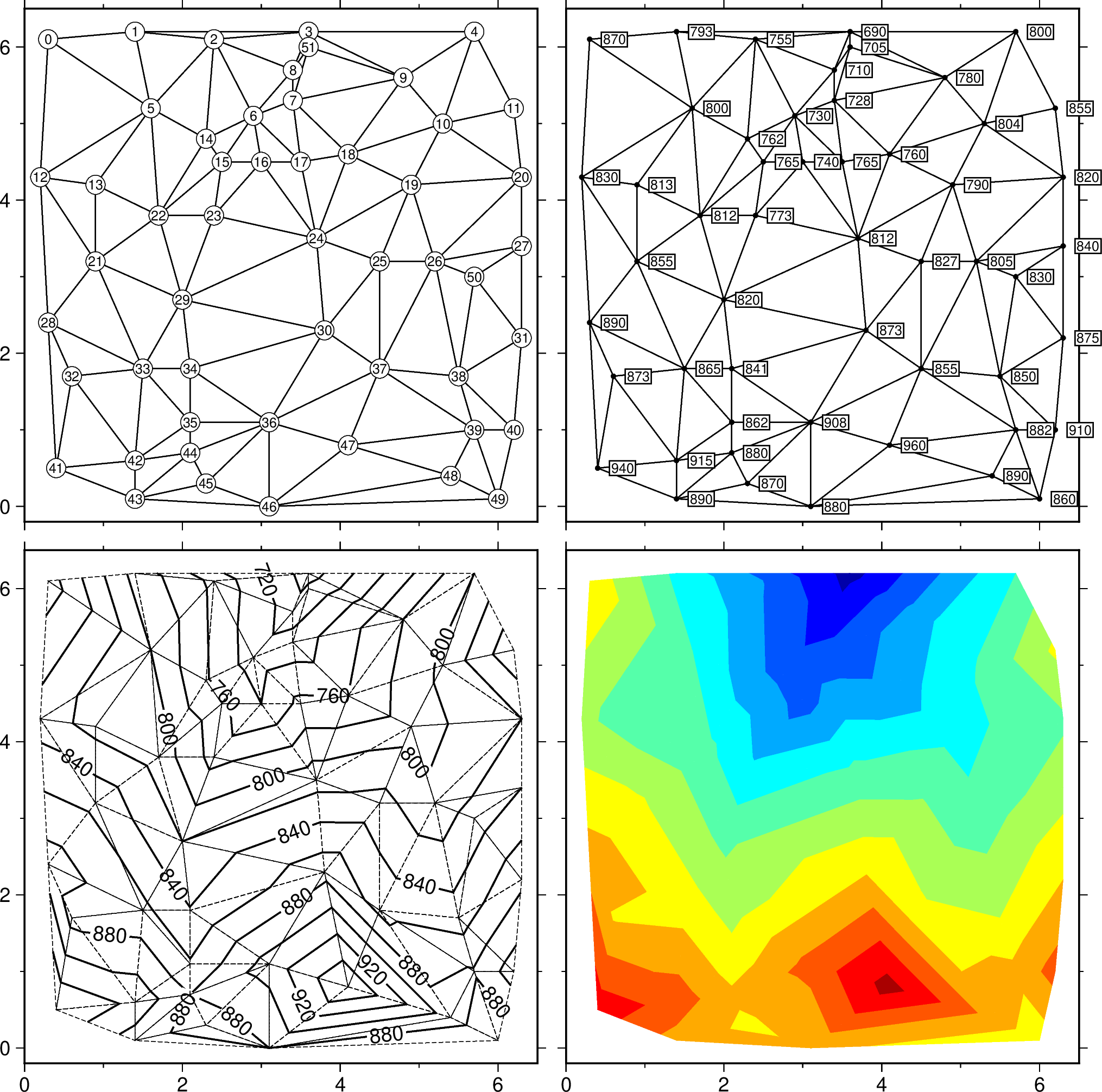
(12) Optimal triangulation of data

Our next example operates on a data set of topographic readings non-uniformly distributed in the plane (Table 5.11 in Davis: Statistics and Data Analysis in Geology, J. Wiley). We use triangulate to perform the optimal Delaunay triangulation, then use the output to draw the resulting network. We label the node numbers as well as the node values, and call contour to make a contour map and image directly from the raw data. Thus, in this example we do not actually make grid files but still are able to contour and image the data. We use the CPT topo.cpt (created via gmtinfo and makecpt). The script becomes:

using GMT

table_5 = gmtread("@Table_5_11.txt")    # The data used in this example
T = gmtinfo(table_5, nearest_multiple=(dz=25, col=2))
makecpt(color=:jet, range=T.text[1][3:end])  # Make it also the current cmap

subplot(grid=(2,2), limits=(0,6.5,-0.2,6.5), col_axes=(bott=true,), row_axes=(left=true,),
        figsize=8, margins=0.1, panel_size=(8,0), tite="Delaunay Triangulation")
	# First draw network and label the nodes
	net_xy = triangulate(table_5, M=true)
	plot(net_xy, lw=:thinner)
	plot(table_5, marker=:circle, ms=0.3, fill=:white, MarkerLine=:thinnest)
	text(table_5, font=6, rec_number=0)

	# Then draw network and print the node values
	plot(net_xy, lw=:thinner, panel=(1,2))
	plot(table_5, marker=:circle, ms=0.08, fill=:black)
	text(table_5, zvalues=true, font=6, justify=:LM, fill=:white, pen="", clearance="1p", offset=("6p",0), noclip=true)

	# Finally color the topography
	contour(table_5, pen=:thin, mesh=(:thinnest,:dashed), labels=(dist=2.5,), panel=(2,1))
	contour(table_5, colorize=true, panel=(2,2))
subplot("show")